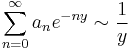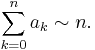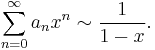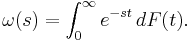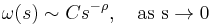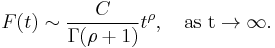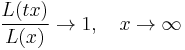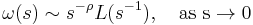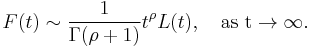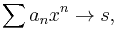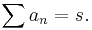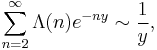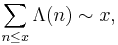Hardy–Littlewood tauberian theorem
In mathematical analysis, the Hardy–Littlewood tauberian theorem is a tauberian theorem relating the asymptotics of the partial sums of a series with the asymptotics of its Abel summation. In this form, the theorem asserts that if, as y ↓ 0,
then
The integral formulation of the theorem relates in an analogous manner the asymptotics of the cumulative distribution function of a function with the asymptotics of its Laplace transform.
The theorem was proved in 1914 by G. H. Hardy and J. E. Littlewood.[1]:226 In 1930 Jovan Karamata gave a new and much simpler proof.[1]:226
Contents |
Statement of the theorem
Series formulation
This formulation is from Titchmarsh.[1]:226 Suppose an ≥ 0 for all n, and as x ↑ 1 we have
Then as n goes to ∞ we have
The theorem is sometimes quoted in equivalent forms, where instead of requiring an ≥ 0, we require an = O(1), or we require an ≥ −K for some constant K.[2]:155 The theorem is sometimes quoted in another equivalent formulation (through the change of variable x = 1/ey ).[2]:155 If, as y ↓ 0,
then
Integral formulation
The following more general formulation is from Feller.[3]:445 Consider a real-valued function F : [0,∞) → R of bounded variation.[4] The Laplace–Stieltjes transform of F is defined by the Stieltjes integral
The theorem relates the asymptotics of ω with those of F in the following way. If ρ is a non-negative real number, then the following are equivalent
Here Γ denotes the Gamma function. One obtains the theorem for series as a special case by taking ρ = 1 and F(t) to be a piecewise constant function with value 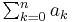 between t=n and t=n+1.
between t=n and t=n+1.
A slight improvement is possible. A function L(x) is slowly varying at infinity if
for every positive t. Let L be a function slowly varying at infinity and ρ a non-negative real number. Then the following are equivalent
Examples
Littlewood's extension of Tauber's theorem
In 1911 Littlewood proved an extension of Tauber's converse of Abel's theorem. Littlewood showed the following: If an = O(1/n ), and as x ↑ 1 we have
then
This came historically before the Hardy–Littlewood tauberian theorem, but can be proved as an simple application of it.[1]:233–235
Prime number theorem
In 1915 Hardy and Littlewood developed a proof of the prime number theorem based on their tauberian theorem; they proved
where Λ is the von Mangoldt function, and then conclude
an equivalent form of the prime number theorem.[5]:34–35[6]:302–307 Littlewood developed a simpler proof, still based on this tauberian theorem, in 1971.[6]:307–309
Notes
- ^ a b c d Titchmarsh, E. C. (1939). The Theory of Functions (2nd ed.). Oxford: Oxford University Press. ISBN 0198533497.
- ^ a b Hardy, G. H. (1991) [1949]. Divergent Series. Providence, RI: AMS Chelsea. ISBN 0828403341.
- ^ Feller, William (1971). An introduction to probability theory and its applications. Vol. II.. Second edition. New York: John Wiley & Sons. MR0270403.
- ^ Bounded variation is only required locally: on every bounded subinterval of [0,∞). However, then more complicated additional assumptions on the convergence of the Laplace–Stieltjes transform are required. See Shubin, M. A. (1987). Pseudodifferential operators and spectral theory. Springer Series in Soviet Mathematics. Berlin, New York: Springer-Verlag. ISBN 978-3-540-13621-7. MR883081.
- ^ Hardy, G. H. (1999) [1940]. Ramanujan: Twelve Lectures on Subjects Suggested by his Life and Work. Providence: AMS Chelsea Publishing. ISBN 9780821820230.
- ^ a b Narkiewicz, Władysław (2000). The Development of Prime Number Theory. Berlin: Springer-Verlag. ISBN 3540662898.
External links
- Hazewinkel, Michiel, ed. (2001), "Tauberian theorems", Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=t/t092280
- Weisstein, Eric W., "Hardy-Littlewood Tauberian Theorem" from MathWorld.